주요 수간곡선식 비교에 따른 남부지역 곰솔 수간재적표 개발
Ⓒ The Korean Environmental Sciences Society. All rights reserved.
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This study was carried out for the purpose of selecting the most appropriate taper equation for the actual stands of Pinus thunbergii in the southern coastal region of Korea and then developing a stem volume table to provide basic data for rational management. To develop a volume table of Pinus thunbergii in this region of Korea, 59 sample trees with various diameter distributions were selected and stem analysis was performed. As a result of stem analysis, two trees with abnormal diameter and height growth as the age increased were rejected, and 57 trees were analyzed. To develop the taper equation, seven major variable exponential equations were used, including Kozak 1988, 1994, 2001, 2002, Bi 2000, Muhairwe 1999, and Sharma and Parton 2009. As a result of parameter estimation and statistical verification, the Kozak 1988 model showed the highest goodness of fit with Fit I (Fit Index), RMSE 1.5620, Bias 0.0031, and MAD 1.0784. The diameter of each 10cm stem ridge for the selected model was estimated, and a stem volume table was produced using the mensuration of division (end area formula) using the Smalian equation. As a result of two-sample T-test for volume table of this study and current yield table, the volume for this study was found to be significantly larger at all observation points (p < 0.001). Even for the same tree species, it is judged that differentiated volume tables are needed for each growth environment characteristic.
Keywords:
Pinus thunbergii Parl., Sectional measurement, Taper equation, Volume table1. 서 론
재적표(volume table)는 산림경영에서 목재생산계획 수립 및 생산량 추정에 직접적인 입목의 재적 정보를 제공하는 자료이다. 이러한 재적표는 자료수집 범위에 따라 일반적 재적표와 지방적 재적표로 구분되며, 우리나라의 경우 주요 수종에 대한 일반적 재적표가 개발되어 있고 소나무는 강원지방소나무와 중부지방소나무로 구분하여 지방적 재적표가 개발되어 있다. 현재 우리나라의 재적표는 수간곡선식(taper equation)을 통해 추정된 수간형상을 Smalian 식에 의한 구분구적법(sectional measurement)으로 재적을 계산하여 작성한다(Kim, 2022).
수간곡선식의 발전과 역사에서 일반적으로 세 가지 범주로 구분할 수 있다. 첫 번째, 단일 수간곡선식(Kozak et al., 1969; Ormerod et al., 1973; Reed and Byrne, 1985; Sharma and Oderwald, 2001)은 간단한 수학적 방정식으로 구성되어 있으며, 수간의 근주 부위가 표현되지 않는 단점이 있다. 두 번째, 분할 수간곡선식(Max and Burthart, 1976; Demaerschalk and Kozak, 1977; Cao et al., 1980; Border and Bailey, 2000)은 수간의 서로 다른 부분을 나타내는 여러 다항식이 변곡점(inflection point)을 통해 연결되며, 원주, 포물선 및 나일로이드체로 구분된다. 세 번째, 가변형태(variable-exponent)의 수간곡선식(Kozak, 1988; Newnham, 1992; Bi, 2000; Sharma and Zhang, 2004)은 연속함수에서 독립변수 지수의 변화를 통해 수간 형상을 잘 추정할 수 있으며, 이는 이론적으로 모든 형태의 수간에 적용할 수 있다. 최근에는 지상라이다(terrestrial laser scanning)를 이용하여 수간의 형태를 정확하게 추출하는 연구가 활발하게 진행 중이다(Heinzel and Huber, 2017; Saarinen et al., 2017; Luoma et al., 2019).
곰솔(Pinus thunbergii Parl.)은 바닷가와 해풍의 영향이 미치는 곳에서 자생하고 있으며, 북위 29° 00′에서 41° 34′까지 분포하고 있다(Kim and Kil, 1983). 우리나라 해안지역의 주요 조림수종 중 하나로서(Kim, 2003), 중부 이남의 해안지역에 주로 분포하고 동해안 강원도 고성군까지 분포하고 있으며(Kim et al., 1981), 해안의 경관자원으로써 휴양림의 기능뿐 아니라 방풍 및 비사방지 등 해안 방재의 기능도 지니고 있으며, 산림생산력이 소나무나 리기다소나무에 비해 높다(Kim et al., 1986).
현재 우리나라 재적표의 경우 한 종류의 수간곡선 모델(Kozak, 1988)을 이용하여 수간곡선을 형상화하여 제작되고 있어, 실제 수간의 형상이 해당 모델에 대한 적합도가 낮을 경우 실제 재적과 추정 재적의 차이가 발생할 수 있다. 또한 우리나라 곰솔림의 평균 임령이 높아지고, 간재적이 증대됨에 따라 수간의 형상을 대표할 수 있는 다양한 모델에 대한 검증이 필요한 실정이다. 따라서 본 연구는 우리나라 남부 해안지역 곰솔 현실림을 대상으로 7개의 주요 수간곡선 모델을 이용하여 최적의 수간곡선식 추정에 따른 신규 재적표를 제작하여 합리적인 곰솔 임분 경영을 위한 기초자료 제공을 목적으로 실행되었다.
2. 재료 및 방법
2.1. 분석자료
우리나라 남부지역 곰솔 재적표 개발을 위해 직경분포가 다양한 59본의 대상목을 선정하여 수간석해를 실행하였으며, 수간석해 결과, 수령의 증가에 따른 직경과 수고 생장이 비정상적인 표준목 2본을 기각하여 57본을 대상으로 분석하였다. 수간고별 원판을 추출하여 총 544개의 관측치를 분석자료로 사용하였으며, 개체목의 생장과정을 정밀하게 분석하기 위해 1년 단위로 연륜의 생장량을 측정하였다. 재적표 개발을 위해 선별된 표준목의 평균 수령은 43년, 흉고직경은 22.5 cm, 수고는 14.6 m로 나타났다(Table 1).
2.2. 수간곡선식 개발
본 연구는 수간곡선식 개발을 위해 Kim et al.(2022)이 주요 수간곡선모델 비교에 따른 삼나무 수간재적표 개발에 사용한 Kozak 1988, 1994, 2001, 2002, Bi 2000, Muhairwe 1999 및 Sharma and Parton 2009 등 7개의 주요 변량지수식(variable-exponent taper equation)을 선택하였다(Table 2). 여러 수간곡선 모델 형식을 비교하는 대부분의 연구에서는 가변 형식이 줄기 프로필과 부피를 모두 예측하는 과정에서 상대적으로 우수한 성능을 발휘한다는 사실을 확인하였다(Rojo et al., 2005; Li and Weiskittel, 2010). Kozak 1988 모델은(Kozak, 1988) 줄기의 나일로드체(neiloid), 포물선체(paraboloid) 및 원뿔(conic) 형태를 설명하는 변화지수(changing exponent)를 사용하여 현재 변량지수식으로 알려져 있는 모델로 우리나라 주요 수종에 대한 일반적 재적표 제작에 이용되고 있다. 이후 Kozak 1988을 기반으로 대부분의 수종에 적용할 수 있는 새로운 Kozak 1994 모델을 개발하였으나, 다중공선성(multicollinearity)과 자기상관(autocorrelation)에 의한 통계적 검증단계 이후 예측성능은 향상되지 않는다고 보고한 바 있다(Kozak, 1997). Kozak 2001과 2002 역시 Kozak 1988을 기반으로 만들어졌으며, 기존 Kozak 1988 및 1994와 비교하였을 때 다중공선성이 낮다는 장점이 있다(Kozak, 2004). Kozak 2002 모델의 경우 식의 구조가 복잡해 보이지만 로그를 적용하면 쉽게 선형모델로 변환할 수 있다(McTague and Weiskittel, 2021).
Muhairwe 1999 모델은 변곡점에 대한 추정치를 제거하기 위해 Kozak 1988 모델을 수정한 형태를 기반으로 개발되었다(Muhairwe, 1999). Bi(2000)는 삼각법을 이용한 새로운 가변형태(variable-form)의 수간곡선식을 개발하였으며, 식의 앞부분에 있는 세 개의 삼각변수는 수간고별 수간형태의 변화를 나타내고 뒷부분 세 개의 변수는 크기가 다른 수목 사이의 수간형태 차이를 구분하기 위해 사용되었다. Sharma and Parton 2009 모델은 비교적 최근에 개발된 모델로 차원해석(dimensional analysis)적 접근방법을 이용하여 수간곡선식을 전개하였다. 해당 모델은 식의 구조가 간단하여 계수 추정에 편의성을 갖고 있으며, 해당 식에서 지수는 수간고별 수간형태의 변화를 나타낸다(Sharma and Parton, 2009).
각 모델의 최적 함수 도출을 위해 통계프로그램 SAS ver. 9.4의 PROC NLIN 프로시저의 비선형 최소자승 회귀(nonlinear least squares regression)분석을 실시하였다.
2.3. 통계적 검정
본 연구에서 개발된 7개 주요 수간곡선식 계수의 적합성 검증을 위해 Kim et al.(2022)의 연구에서 모델 검증과정에 사용한 결정계수(coefficient of determination), 오차제곱근(root mean square error), 평균절대편차(mean absolute deviation) 및 편의(bias)를 분석하였으며(Table 3), 각 모델의 적합성 검증 결과를 비교하여 우리나라 남부지역 곰솔에 가장 적합한 수간곡선식을 선별하였다.
3. 결과 및 고찰
3.1. 수간곡선식 모수 추정
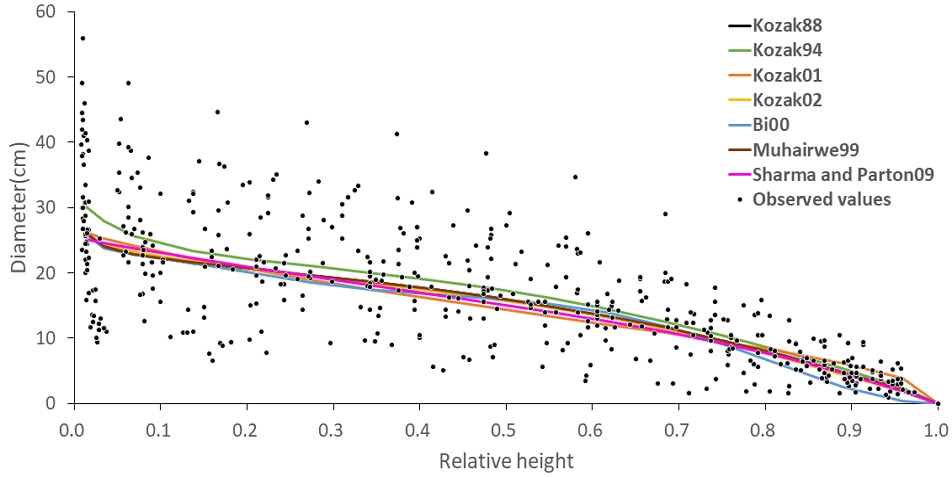
우리나라 주요 수종에 대한 재적표는 Kozak 1988 모델을 사용하고 있으며(National Institute of Forest Science, 2020), 이때 변곡점은 0.25이다. Fig. 1은 실제 본 연구에서 관측된 수간고별 직경분포와 개발된 수고곡선식의 관계를 나타낸 것으로 상대수고 25% 지점에서 나일로이드체가 포물선체로 바뀌는 것이 확인되어 Kozak 1988 모델에 대한 변곡점을 0.25로 결정하였다.
7개의 주요 변량지수식에 대한 비선형 최소자승 회귀분석에 의해 추정된 계수 값은 Table 4와 같다. Kozak 1988, 1994, 2001, 2002 및 Muhairwe 1999 모델의 표준지 및 임목 수준의 특성을 나타내는 매개변수 a1 ~ a3가 유사하게 분석되었다.
모수 추정 결과에 따른 각 모델의 수간곡선과 수간고별 직경의 실측치를 비교한 결과, Kozak 1994 모델의 경우 근주부부터 상대수고 80% 지점까지 다른 모델에 비해 직경이 큰 것으로 나타났다(Fig. 1). 이는 Kozak 1994 모델의 다중공선성 문제 때문이며, 이러한 다중공선성 문제는 일부 설명변수(수간고별 직경)와 다른 설명변수 간의 높은 상관관계에 의해 발생한 것으로 판단된다. Bi 2000 모델의 경우 상대수고 80% 이후에서 다른 모델에 비해 직경의 감소폭이 큰 것으로 나타났으며, 이는 처음 세 개의 삼각변수가 수간 형상의 변화를 묘사하고 있기 때문이라고 판단된다.
3.2. 적합성 검정
7개의 주요 변량지수식에 대한 통계적 검증 결과는 Table 5와 같으며, 우리나라 남부지역 곰솔의 수간형상에 가장 적합한 모델은 Kozak 1988인 것으로 나타났다. Kozak(2004)의 연구에 따르면 Kozak 2001 모델은 가장 단순하며, Kozak 2002 모델이 최상의 예측을 제공할 것으로 예측하였다. 본 연구에서 Kozak 모델 중 2001모델의 적합도는 가장 낮았으나, 2002 모델이 가장 높을 것이라는 예측은 우리나라 남부지역 곰솔에 해당되지 않았다.
Kozak 1988모델에 이어 2002와 1994 모델이 높게 나타났으며, Kozak 2001 모델은 간편식으로 7가지 모델 중 가장 낮게 나타났다. Muhairwe 1999 모델은 우리나라 강원도와 경상북도 지역 잣나무(Lee et al., 2017), 제주도 지역 삼나무(Kim et al., 2022) 및 중국 남부지역 Betula alnoides(Tang et al., 2017)에 대한 수간곡선식 비교연구에서 적합도가 가장 높게 보고된 바 있으며, 해당 연구에서도 적합도가 높게 분석됐으나, 간편식을 제외한 3개의 Kozak 모델보다 상대적으로 적합도가 낮게 나타났다.
3.3. 지방적 수간재적표 제작
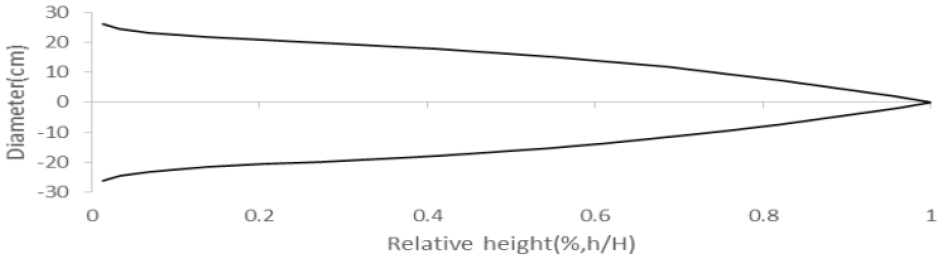
수간곡선식의 모수 추정에 따른 통계적 검증 결과 적합성이 가장 높은 Kozak 1988 모델을 통해 수간형상 및 지방적 수간재적표를 제작하였다(Fig. 2, Table 6). 수간형상은 상대수고 1을 기준으로 수간고별 직경을 통해 도식화하였다. 수간재적표는 흉고직경 6 ~ 30 cm의 범위에 대해 2 cm 괄약(rounding off)을 적용하였고 수고는 5 ~ 25 m의 범위에 대해 1 m 괄약을 적용하였다. 수간재적은 10 cm 수간고별 직경을 추정하고, Smalian식에 의한 구분구적법(양단면적법)으로 산출하였다(Seo et al., 2015; Kang et al., 2015).
3.4. 일반적 수간재적표와 비교검정
본 연구를 통해 제작된 우리나라 남부지역 곰솔 수간재적표를 현재 수확표 상의 수간재적표(National Institute of Forest Science, 2020)와 비교하였다(Table 7). 동일한 흉고직경과 수고에서의 재적에 대한 T-test를 실행한 결과, 모든 관측 지점에서 본 연구의 곰솔 수간재적표가 수확표 상의 수간재적표보다 크게 나타났다(p < 0.05).
본 연구의 경우 남부 해안지역, 즉 곰솔 자생지에서 각 직경급의 표준목에 해당하는 입목을 선별하여 수간석해를 실행하여, 우리나라 전체에 해당하는 일반적 재적표보다 수간의 형상이 통직한 것으로 판단된다. Thomas et al.(2015)는 바람이 많이 부는 열대우림과 일반적인 열대우림에 대한 17종의 속씨식물의 생장을 분석한 결과, 바람이 많이 부는 열대우림 우세목의 점근 높이가 30 ~ 116% 낮은 것으로 보고한 바 있다. 비교적 바람이 많이 부는 해안지역 곰솔의 경우 생장과정에서 직경생장에 비해 초두부 피해에 의한 수고신장 저해로 통직한 형태의 간곡선이 나타난 것으로 판단된다.
4. 결 론
본 연구는 우리나라 남부 해안지역 곰솔에 대하여 지역적 생육환경 및 현실임분의 생장특성을 반영할 수 있는 차별화된 수간재적표를 개발하고자 수행되었다. 재적표 개발을 위해 Kozak 1988, 1994, 2001, 2002, Bi 2000, Muhairwe 1999 및 Sharma and Parton 2009 등 7가지의 변량지수 수간곡선 모델에 대한 모수를 추정하였다. 모수 추정에 따른 통계적 검정 결과, 최적합식으로 선정된 Kozak 1988 모델을 이용하여 재적표를 제작하였다.
Kozak 1988 모델은 Kozak에 의해 만들어진 최초의 변량지수식이며, 이후 이러한 모델을 보완하기 위해 Kozak 1994, 2001, 2002 모델이 개발되었다. 그러나 여러 수간곡선식의 비교 연구 중 Kozak 1988 모델의 적합도가 상대적으로 높다고 보고된 바 있으며, 현재 우리나라 주요 수종에 대한 일반적 재적표에 사용될 만큼 우수한 모델이라고 할 수 있다. 본 연구에서 개발한 우리나라 남부 해안지역 곰솔의 수간재적표에 가장 적합한 모델로 Kozak 1988 모델이 선정되어 수간석해목의 수간고별 직경만을 독립변수로 수확표 상의 곰솔 수간재적표와 비교할 수 있었다. 현재 수확표상의 곰솔 수간재적표와 비교를 위한 t-test를 실행한 결과, 모든 관측 지점에서 본 연구의 수간재적표 재적이 수확표 상의 수간재적표 재적보다 유의적으로 크게 나타났다(p < 0.05). 이를 통해 동일한 수종이라도 생육 범위에 따른 생장특성이 다르며, 합리적 의사결정 및 산림경영을 위한 지방적 재적표가 필요한 것으로 판단되었다.
입목의 생장예측은 생산목표 결정에 따른 목표림형 설정 및 산림 관리・자원 지속성 확보를 위한 중요한 부분으로 정확하게 산출되어야 한다. 본 연구에서 우리나라 곰솔의 생육환경 특성에 따라 동일한 수종 내에서 생장형태가 다른 것을 확인할 수 있었다. 앞으로의 연구에서 우리나라 주요 수종에 대한 생육환경 특성 및 지역적 차이에 따른 정도 높은 재적표를 제작한다면 합리적인 산림자원 관리에 필요한 정보제공이 가능할 것으로 판단된다. 또한, 적합성을 높일 수 있는 더 많은 모델 적용과 기존 모델의 적합도를 높일 수 있는 보완 및 신규 모델의 개발이 필요할 것이다. 현재 우리나라 재적표의 경우 일부 주요 수종에 대해 제작되고 있으나, 기후변화에 따른 생육분포의 변화에 대비하기 위한 난대・아열대 산림 수종에 대한 생육환경에 따른 생장 특성 및 수간재적표 제작과 관련된 연구가 활발히 이루어져야 할 것으로 판단된다.
Acknowledgments
본 연구는 산림청 일반연구사업(과제번호: SC0600-2021-01)의 일부 지원으로 이루어진 것입니다.
REFERENCES
-
Bi, H., 2000, Trigonometric variable-form taper equations for Australian eucalyptus, For. Sci., 46, 397-409.
[https://doi.org/10.1093/forestscience/46.3.397]

-
Borders, E., Bailey, L., 2000, Compatible volume-taper models for loblolly and slash pine based on a system with segmented-stem form factors, For. Sci., 46, 1–12.
[https://doi.org/10.1093/forestscience/46.1.1]

- Cao, Q. V., Burkhart, H. E., Max, T. A., 1980, Evaluation of two methods for cubic-volume prediction of loblolly pine to any merchantable limit, For. Sci., 26, 71–80.
-
Demaerschalk, J., Kozak, A., 1977, The whole-bole system: A Conditioned dual-equation system for precise prediction of tree profiles, Can. J. For. Res., 7, 488–497.
[https://doi.org/10.1139/x77-063]

-
Heinzel, J., Huber, M. O., 2017, Detecting tree stems from volumetric TLS data in forest environments with rich understory, Remote Sensing, 9(1), 9.
[https://doi.org/10.3390/rs9010009]

- Kang, J. T., Moon, H. S., Son, Y. M., Ahn, K. W., 2015, An Estimation on the stem volume of Cryptomeria japonica in Jeju using Kozak’s stem taper model, Journal of Korean Island, 27(3), 145-160.
-
Kim, H. S., Jung, S. Y., Lee, K. S., 2022, Evaluation of major taper equation models for developing a stem volume table of Cryptomeria japonica in Jeju Island, Journal of Environmental Science International, 31(11), 941-950.
[https://doi.org/10.5322/JESI.2022.31.11.941]

- Kim, J. U., Kil, B. S., 1983, A Study on the distribution of Pinus thunbergii in the Korean peninsula, Kor. J. Eco., 6, 45-54
- Kim, J. U., Yim, Y. J., Kim, B. S., 1986, Changes of site index and production of black pine (Pinus thunbergii Parl.) stand from coast to inland, Korean Journal of Ecology, 9, 123-133.
- Kim, S. H., 2003, Ecological characteristics of Japanese black pine (Pinus thunbergii) forests of east coastal sand dunes in Korea, Ph.D. Thesis, Seoul Nat. Univ., Korea.
-
Kim, Y. S., Ko, S. C., Choi, B. H., 1981, Distribution atlas of plants of Korea, Kor. J. Pl. Taxon., 11, 53-76.
[https://doi.org/10.11110/kjpt.1981.11.1.053]

-
Kozak, A., 1988, A Variable-exponent taper equation, Can. J. For. Res., 18, 1363–1368.
[https://doi.org/10.1139/x88-213]

-
Kozak, A., 1997, Effects of multicollinearity and autocorrelation on the variable-exponent taper functions. Can. J. For. Res., 27(5), 619-629.
[https://doi.org/10.1139/x97-011]

-
Kozak, A., 2004, My last words on taper equations, Forestry Chronicle, 80(4), 507-515.
[https://doi.org/10.5558/tfc80507-4]

-
Kozak, A., Munro, D., Smith, J., 1969, Taper functions and their application in forest inventory, Forestry Chronicle, 45, 278–283.
[https://doi.org/10.5558/tfc45278-4]

- Lee, D. S., Seo, Y. W., Lee, J. H., Choi, J. K., 2017, Estimation and validation of taper equations for three major coniferous species in Gangwon and North Gyeongsang provinces of South Korea, Journal of Forest and Environmental Science, 33(4), 315-321.
-
Li, R., Weiskittel, A. R., 2010, Comparison of model forms for estimating stem taper and volume in the primary conifer species of the North American Acadian Region, Journal of Forest Science, 67, 302.
[https://doi.org/10.1051/forest/2009109]

-
Luoma, V., Saarinen, N., Kankare, V., Tanhuanpää, T., Kaartinen, H., Kukko, A., Holopainen, M., Hyyppä, J., Vastaranta, M., 2019, Examining changes in stem taper and volume growth with two-date 3D point clouds, Forests, 10, 382.
[https://doi.org/10.3390/f10050382]

- Max, T. A., Burkhart, H. E., 1976, Segmented polynomial regression applied to taper equations, For. Sci., 22, 283–289.
-
McTague, J. P., Weiskittel, A., 2021, Evolution, history, and use of stem taper equations: A Review of their development, application, and implementation, Can. J. For. Res., 51, 210–235
[https://doi.org/10.1139/cjfr-2020-0326]

-
Muhairwe, C. K., 1999, Taper equations for Eucalyptus pilularis and Eucalyptus grandis for the north coast in New South Wales, Australia, Forest Ecological Management, 113, 251-269.
[https://doi.org/10.1016/S0378-1127(98)00431-9]

- National Institute of Forest Science, 2020, Stand volume・biomass and stand yield table, Seoul, Korea, 361.
-
Newnham, R., 1992, Variable-form taper functions for four alberta tree species, Can. J. For. Res., 22, 210–223.
[https://doi.org/10.1139/x92-028]

-
Ormerod, D. A., 1973, Simple bole model, Forestry Chronicle, 49, 136–138.
[https://doi.org/10.5558/tfc49136-3]

-
Reed, D. D., Byrne, J. C., 1985, A Simple, variable form volume estimation system, Forestry Chronicle, 61, 87–90.
[https://doi.org/10.5558/tfc61087-2]

-
Rojo, A., Perales, X., Sanchez-Rodriguez, F., Alvarez-Gonzalez, J.G., Gadow, K., 2005, Stem taper functions for maritime pine (Pinus pinaster Ait.) in Galicia (Northwestern Spain), Eur. J. For. Res., 124(3), 177–186.
[https://doi.org/10.1007/s10342-005-0066-6]

-
Saarinen, N., Kankare, V., Vastaranta, M., Luoma, V., Pyörälä, J., Tanhuanpää, T., Liang , X., Kaartinen, H., Kukko, A., Jaakkola, A., Yu, Xiaowei., Holopainen, M. and Hyyppä, J., 2017, Feasibility of Terrestrial laser scanning for collecting stem volume information from single trees, Journal of Photogrammetry and Remote Sensing, 123, 140-158.
[https://doi.org/10.1016/j.isprsjprs.2016.11.012]

-
Seo, Y. O., Jung, S. C., Won, H. K., Lee, Y. G., 2015, Taper equation and stem volume table of Cryptomeria japonica in Jeju experimental forests, Journal of Agriculture & Life Science, 49(1), 71-77.
[https://doi.org/10.14397/jals.2015.49.1.71]

-
Sharma, M., Parton J., 2009, Modeling stand density effects on taper for jack pine and black spruce plantations using dimensional analysis, Forest Science, 55, 268-282.
[https://doi.org/10.1093/forestscience/55.3.268]

-
Sharma, M., Zhang, S. Y., 2004, Variable-exponent taper equations for jack pine, black spruce, and balsam fir in eastern Canada, For. Ecol. Manag., 198, 39–53.
[https://doi.org/10.1016/j.foreco.2004.03.035]

-
Sharma, M., Oderwald, R. G., 2001, Dimensionally compatible volume and taper equations, Can. J. For. Res., 31, 797–803.
[https://doi.org/10.1139/x01-005]

- Tang, C., Wang, C. S., Pang, S. J., Zhao, Z. G., Guo, J. J., Lei, Y. C., Zeng J., 2017, Stem taper equations for Betula alnoides in South China, Journal of Tropical Forest Science, 29(1), 80-92.
-
Thomas, S. C., Martin, A. R., Mycroft, E. E., 2015, Tropical trees in a wind-exposed island ecosystem: Height-diameter allometry and size at onset of maturity, Journal of Ecology, 103, 594–605.
[https://doi.org/10.1111/1365-2745.12378]

Division of Warm Temperate and Subtropical Forest Research Center, National Institute of Forest Sciencekhsggam1@korea.kr
Division of Warm Temperate and Subtropical Forest Research Center, National Institute of Forest Sciencesuyoung.jung@korea.kr
Division of Warm Temperate and Subtropical Forest Research Center, National Institute of Forest Sciencebeldel660@korea.kr