Weibull 직경분포모델을 이용한 편백림의 경험적 임분수확표 개발

1. 서 론

산림 내 임목의 생장과 수확에 대한 연구는 아주 오래전으로 거슬러 올라가는데, 1787년 독일에서 처음으로 임분수확표가 문헌으로 출판되었고, 이후 100년 동안 1,000개 이상의 수확표가 만들어졌다. 현재의 수확표는 수확 뿐만아니라 수고, 직경, 흉고단면적, 연년생장량 등 다양한 정보를 제공하고 있다(Vuokila, 1965; Vanclay, 1994). 지역별로 볼 때, 유럽은 1850년대초 중부 유럽 숲의 생장과 수확량을 모델링하기 위하여 도해법(Graphic method)을 이용하였고, 미국은 이보다 늦은 1920~40년대에 기준곡선법(Guide curve method)을 임분수확표에 적용하였다(Spurr, 1952; Monserud, 1984; Peng, 2000). 이런 모델은 1950년대까지 이어졌으며, 이후 정보 및 기술력의 발전으로 모델링의 복잡성과 효과성의 해석이 비약적으로 발전하기 시작하였다. 특히 첫 IUFRO 개최에 따른 성과와 호환가능한 생장모델 들이 개발되면서 산림생장 및 수확에 대한 이해력이 가속화되기 시작하였다(Buckman, 1962; Fries, 1974).

수확표는 법정수확표(Normal yield table)와 현실적 또는 경험적 수확표(Actual or empirical yield table)로 크게 구분하는데, 전자는 충분한 입목도를 가지는 임분의 정상적인 생장과정을 전제로 규범적인 수확량을 기술한 반면, 후자는 현실림의 평균 수확량을 나타내는 실용적인 것으로 독립변수는 임령과 지위 외에 각종 임분밀도가 이용되어 가변밀도수확표(Variable density yield table)라고도 불린다(Spurr, 1952; Leary, 1991; Vanclay, 1994)

우리나라에서 수확표 작성 연구가 처음 시작된 것은 일본인 Hayashi(1937)가 낙엽송림에 대하여 임령 5~30년까지 지위지수별 수확표를 작성한 것이 최초이며, 정부 수립 이후 1960년대에서 1970년대까지 소나무, 낙엽송, 잣나무, 참나무 등 9개 수종에 대하여 10~50년까지 5년 간격으로 지위지수별, 주ㆍ부림목별로 수확표를 작성한 바 있다(Kim et al., 1977). 또한 곰솔, 상수리, 신갈나무림에 대한 수확표를 임령 70년까지로 확대하여 조제하기도 하였다(Lee et al., 1985; Lee et al., 1996). 한편, 2001년부터 국립산림과학원에서는 잣나무 등 우리나라 주요 8개 수종에 대하여 Weibull 직경분포모델을 이용하여 수확표를 작성하는 최신 분석기법을 도입하였다. 2009년에 출간된 임분수확표는 침엽수 8종, 활엽수 3종, 총 11종의 임분생장 정보를 제공하여 1985년 이후 처음으로 수확표가 새롭게 제작이 되었다(NIFoS, 2009). 이후 굴참나무, 자작나무 등의 활엽수를 보강한 수확표가 2012년에 다시 제작되었으며, 이후 최근까지 지속적인 보완 작업에 의해 개정판이 보급되고 있다(Son et al., 2004; NIFoS, 2012, 2023).

우리나라의 편백은 남부지역 대표 수종으로 Kim et al.(1977)에 의하여 기존에 수확표가 작성된 바 있다. 다만 초기에는 임령의 범위를 55년까지 잡아 정보를 제공하였고, 이후 국립산림과학원에서는 70~80년 범위를 일부 포함하는 정보를 제공하였으나, 당시 노령림 자료가 부족하여 제대로 된 정보라고 할 수가 없었다(Forest Research Institute, 1962~1985). 편백림과 관련한 기타 생장·수확 연구로는 간벌에 따른 생장효과, 밀도관리도를 이용한 고사 및 수확량 추정, 지위지수와 적지적수 분석, 임목 수간곡선식 및 재적표 개발, 현실생장을 고려한 수확표 개발 등이 수행되었다(Kang et al., 2015; Park et al., 2018, 2019; Kang et al., 2020; Jung et al., 2020).

본 연구에서는 국가산림자원조사 자료를 활용하여 현실 편백림에 사용가능한 경험적 수확표를 작성하고자 수행하였으며, 분석은 Weibull 직경분포모델을 적용시켜 지위별 임령별 각종 생장량 정보 제시 뿐만아니라 경급별 입목본수 및 재적량 까지도 파악할 수 있도록 하였다.

2. 재료 및 방법

2.1. 공시 재료

편백 수확표 작성을 위해 사용된 표준지 자료는 국가산림조사(National forest inventory, NFI)의 표본점 자료 중 산림경영이 가능한 몇가지 기준조건을 주어 자료를 취합하였다. 즉, 먼저 시업지(Working area)로 구분된 곳을 대상으로 하고, 경영이 가능한 해발고 1,000 m 이하의 표준지를 대상으로 하였다. 그리고 표준지의 대표 수종은 표준지 내 흉고단면적이 75% 이상을 차지하는 수종으로 정하였으며, 그 외는 단일수종으로 취급하지 않았다. 또한 나지(Bareland), 인위적 및 자연적 훼손지 지역의 임령에 따른 평균적 입목본수를 가지지 않는 표준지는 분석자료에서 기각시켰다. 한편 정밀한 임분수확표 도출을 위해서는 각 임령대별로 표준지가 DB화 되어야 하는데, NFI 자료는 이를 모두 충족시킬 수가 없어 유령림과 노령림에 대한 표준지 자료는 산림과학원에서 기존 조사하였던 일부 자료를 포함시켰다.

분석 자료를 산림경영이 가능 임지로 한정한 것은 수확표가 간벌, 벌채, 매각 등에 사용되는 산림경영을 위한 기준표이므로 이렇게 자료를 한정한 것이며, 취합된 표준지 입목생장 개황은 Table 1과 같다.

Table 1.

The general characteristic of survey sites in Chamaecyparis obtusa forest

Table 1에서 표준지의 임령은 최소 8년에서 최대 80년까지 나타났으며, 임분의 평균흉고직경은 20.9 cm, 평균수고는 16.6 m, ha당 평균입목밀도는 1,196본임을 알 수 있었다.

2.2. 분석 방법

2.2.1. Weibull 직경분포모델 적용

편백림의 경영을 위해서는 직경급별 본수 및 재적의 분포 등 임분생장과 임분구조 구명이 중요하므로 Weibull 모델을 이용하였으며, 누적밀도에 관한 수식은 (식 1)과 같다. 이러한 직경분포를 이용한 생장모형에 있어 Weibull 모델은 유연성과 정도 면에서 널리 사용되고 있다(Cao et al., 1984; Liu et al., 2002). Weibull 모델 상 a는 모형의 초기위치를 결정하는데, 대부분 최소직경으로 결정된다. b는 범위의 모수로 직경분포의 범위를 나타내며 c는 모양의 모수로 분포의 모형을 나타낸다(Bailey et al., 1973; Ek et al., 1975). 각 파라미터의 추정은 Garcia(1981)에 의한 단순적률법(Simplified method-of-moments)으로 간단하게 계산할 수 있다. 이 방법은 최소직경, 평균직경, 직경의 표준편차 등에 의해 쉽게 모수를 추정할 수 있으며, 최소직경과 직경의 표준편차는 평균직경과 우세목 수고에 의해 추정이 가능하다(Son et al., 2012). Weibull 모델의 모수에 대한 복구, 예측 등의 적합성 검정은 Kormogrove-Smirnov test (K-S test)로서 실시하였다(Garcia, 1981)

그리고 직경급의 밀도와 본수는 누적 밀도의 차이에 의해 (식 2)로서 계산되며, 본 분석 및 각종 식의 파라미터 도출은 SAS 통계시스템을 활용하였다(Kim, 2000).

$\[ F\left(x\right)=1-\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{x-a}{b}\right)}^c\right] \]$

(Eq. 1)

$\[ P_i=F\left(U_i\right)-F\left(U_{i-1}\right) \]$

(Eq. 2)

(Where is, F(x): Weibull function, a,b,c : Parameters (a≤x$$ \prec $$∞), x : DBH, P_i : a proportion of tree in diameter class I, and U_i : upper limit of diameter class I.)

2.2.2. 임분 생장식 도출

임분수확표 작성을 위해서는 흉고직경, 흉고단면적, 수고, 최대 및 최소직경, 단면적 표준오차 등을 산정할 수 있는 최적식을 도출하여 모델 내에 적용시켜야 한다. 이를 위해서 Chapman-Richards(C-R)식, Schumacher 식, Weibull 식, 일반 지수식, 회귀식 등을 적용시켰으며, 이들 중 적합도 지수(Fitness index, FI)가 가장 높은 식을 최적식으로 선정하였으나, 이들 중 일반적인 생장관계 해석이 불가한 식은 배제하였다. 예를 들자면 식의 적합도 지수는 높게 도출되었으나, 잔차도가 왜곡되거나, 임령 10년 미만을 식에 적용하였을 때, ‘- (Minus)’ 값이 나오는 식은 최적식에서 기각시켰다. 이러한 일련의 절차는 앞서와 마찬가지로 SAS 통계시스템을 활용하였다(Kim, 2000).

Table 2.

Growth equation using parameter inducement of Weibull diameter distribution model

2.2.3. 지위지수식 도출

지위지수를 추정하기 위하여 가장 많은 이용빈도를 보이고 있는 모델은 Chapman-Richards 모델과 Schumacher모델을 들 수 있는데, 이들은 생장식 도출에도 많이 사용되나, 이를 우세목 수고 및 현실림 임령(Actual age), 기준임령(Base age)을 갖는 모델로 약간 변형한 모델이다(Schumacher, 1939; Richards, 1959; Chapman, 1961). C-R모델은 이미 임분생장을 해석하는데 융통성이 널리 알려진 모델로서 본래 모수 a,b,c 의 3개 모수를 가졌으나, 최대값인 점근(Asymptotic)을 갖는 모수 a를 우세목의 수고로 대체한 모델이다(Clutter et al., 1983). Schumacher 모델은 Schumacher(1939)에 의해 처음 임령과 임분수고 간의 관계를 제시한 모델이었는데, 당시 Schumacher는 임령에 따른 수고생장에 변곡점(Inflection point, 수고생장 기울기가 변화되는 시점)이 있다는 점을 간과하였으나, 이후 다른 연구자들이 보완하여 오늘에 이르고 있다(Clutter et al., 1983).

지위지수를 추정할 수 있는 이 모델들은 우리나라의 경우 기준임령 30년일 때의 우세목 수고를 기준으로 하는데, 30년으로 정한 것은 일반적으로 이 시점이 수고 생장이 거의 정점에 이르기 때문이다. 1960~80년대 까지만 해도 우리나라의 수종별 지위지수 추정은 20년을 기준임령으로 하였었다. 본 분석에서는 두 개의 지위지수 추정모델 중 적합도가 높은 것을 채택하여 수확표 도출에 사용하였다.

$\[ SI=H_D{\left[\frac{1-e^{-b{t}_j}}{1-e^{-b{t}_i}}\right]}^c \]$

(eq. 3, C-R 모델)

$\[ SI=\mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{l}\mathrm{n}{H}_D+b\left(\frac{1}{t_i}-\frac{1}{t_j}\right)\right] \]$

(eq. 4, Schumacher 모델)

(Where is, SI : Site index, H_D : Dominant tree height, t_i : Stand age, t_j : Base age(30), b,c : Parameters)

2.2.4. 임분수확표 제작

임분수확표는 Weibull 직경분포모델에 대한 모수추정(Estimation), 복구(Recovery) 및 예측(Prediction) 절차를 거쳐 직경급별 ha당 입목본수 및 재적을 도출하게 되며, 재적은 국립산림과학원에서 Kozak 식에 의해 새롭게 만든 수간곡선식과 파라미터를 적용시켜 도출하였다(NIFoS, 2023). 산림과학원에 의하면 수종별로 수간곡선식을 적용하여 산출한 개체목의 재적이 대부분 수종에서 기존의 재적보다 많이 산정되고 있음을 보고한 바 있다. 이 같은 원인으로는 1960-80년대 재적도출에 사용된 수종별 자료는 대부분이 유령림에서 표준목이 조사되었으며, 그 외 일부 장령림에서의 약간의 자료가 수집되었기 때문에, 현재와 같이 제대로 생장한 개체목의 생장자료가 없던 현실에서 오는 자료수집의 한계라고 볼 수 있다.

Weibull 직경분포모델 기반 하에 상기에서 도출한 각종 추정식을 적용시켜, 지위지수별, 임령별로 생장량을 제시한 것이 바로 임분수확표이다. 본 연구를 통해 제시될 수확표와 ’80년대 이전에 만들어진 수확표 간의 전혀 다른 점은, 이번에 만들 수확표가 Weibull 직경분포모델을 적용시킴에 따라 직경급별 본수 및 재적분포가 도출되는데, 이를 이용하면 간벌에 따른 수확량 및 임분구조 변화를 알 수 있고, 비간벌지와의 생장차이를 평가하고 예측할 수 있다는 장점이 있다.

3. 결과 및 고찰

3.1. Weibull 직경분포모델의 적용

3.1.1. 모델의 모수 추정, 복구 및 예측

모델의 모수를 추정, 복구, 예측하기 위해서 사용되는 다양한 생장식이 있는데, 여기에 적용되는 독립변수들 역시 다양하다. 기본적인 변수는 임령과 지위지수이고, 수고 추정을 위해서는 누적직경밀도(Accumulated diameter density)가 변수로 사용되며, 최소직경 및 최대직경 추정식 도출에는 직경과 우세목 수고, 그리고 흉고단면적 표준편차 추정식에는 앞서 도출한 최대직경과 최소직경이 변수로 투입이 되었다. 이들에 대한 생장식 및 적합도지수는 다음과 같다.

그리고 Weibull 직경분포모델의 모수를 추정하고 복구하는 단계를 거쳐 도출된 표준지별 a, b, c 파라미터를 적용하여 실제 직경분포와 추정 직경분포를 비교한 결과의 정도를 알기 위해 Kormogrove-Smirnov test (K-S test)를 실시하였는데 그 결과는 Table 3과 같다.

Table 3.

K-S value equation by parameter estimation and recovery process of Weibull diameter distribution model

Table 3에서, 표준지별 직경분포를 추정하는 단계에서는 실제 직경분포와 99.1% 적합도를 보임을 알 수 있었고, 최소직경, 최대직경 등을 이용하여 모수를 복구하는 단계에서는 전자보다는 약간 낮은 90.8%의 적합성을 보여 주었다. 이렇게 실제 직경분포를 추정하고, 또 변수를 투입하여 모수복구에 의한 직경분포 추정하는 단계는 결국 지위지수와 임령의 변수로 임분수확표를 만들고 이에 따른 경급별 입목본수 분포 및 재적분포를 추정하기 위한 전 단계라고 볼 수 있다.

3.1.2. Weibull 모델 도출에 따른 직경급별 임분구조 변화

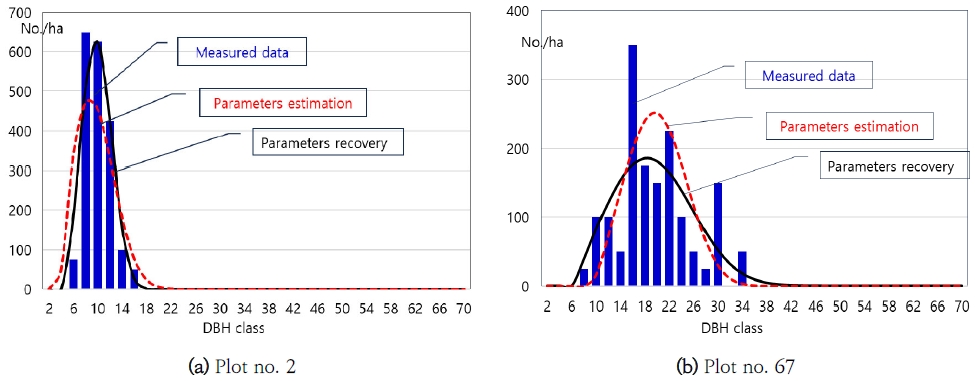
모수 추정 및 복구를 통한 표준지별 직경분포를 일부 몇 개 표준지를 대상으로 표현하면 다음과 같다.

그림 1에서 Weibull 직경분포모델의 모수 a, b, c를 추정하는 단계(Parameter estimation)를 거친 단계와 복구하는 단계(Parameter recovery)를 거친 표준지의 직경분포를 도식화한 결과(예, 표준지 2 및 67번), 모두 실제 직경분포를 거의 설명할 수 있는 수준이었으며, 이는 K-S test 검증 결과(99.1%, 90.8%)가 그림 상에 제대로 표현된 것이라 볼 수 있다.

Fig. 1.

Change of diameter distribution according to the parameter estimation and recovery process of Weibull model.

3.2. 지위지수 추정식 도출 및 분류도 작성

3.2.1. 최적 지위지수 추정식 도출

임분수확표를 제작하기 위해서 각종 생장식도 절차 상 도출함이 당연하지만, 가장 중요한 인자는 지위지수라고 볼 수 있다. 지위지수는 산림경영에 있어 해당 임분의 임지생산력을 나타내 주는 기준이 되므로 이에 따라 경영의 방향이 달라지기 때문이다.

편백 임분의 최적 지위지수 도출을 위해서 C-R 및 Schumacher 모델을 적용시킨 결과, 다음과 같은 통계치가 산출되었다.

Table 4에서, 회귀분석의 결정계수 역할을 같이 하는 적합도지수(FI)는 C-R 모델이 약간 높은 것으로 나왔으며, 상대적인 정도(Accuracy)를 평가하는 추정치 표준오차의 백분율(SEE), 개개 추정치의 평균적인 편차 크기를 나타내 주는 평균절대편차(MAD) 및 추정량이 모수에 대해 어느 정도 과소치 혹은 과대치를 주는 지를 나타내는 편의(Bias) 모두 C-R 모델이 약간씩 우수한 것으로 나타났다. 따라서 편백림의 지위지수 도출을 위한 최적식은 C-R 모델을 선택하였다.

$\[ SI=H_D{\left[\frac{1-e^{-0.0069\times 30}}{1-e^{-0.0069\times age }}\right]}^{0.5167} \]$

(eq. 5, 지위지수 추정 최적모델)

Table 4.

Statistic of site index estimation model applied to the Chamaecyparis obtusa forest

3.2.2. 지위지수분류도

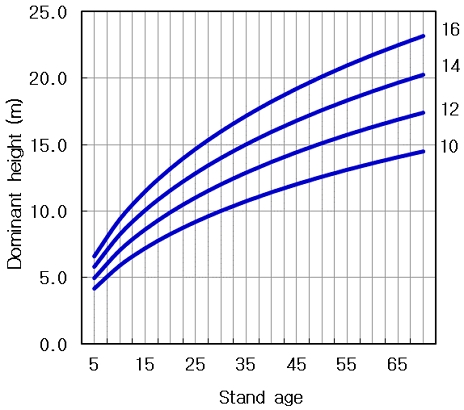
편백림의 임지생산력은 그림 2와 같이 나타낼 수 있으며, 필요에 따라 10 미만, 또는 18 이상으로 확장시켜 표현할 수가 있다. 다만 현재 국가산림조사 자료로 분석한 결과, 우리나라 편백림의 지위지수 분포는 10~16 정도 범위 내에 있는 것으로 나타났다. Jung et al.(2020)은 편백 현실림 지위지수 분류에 있어 국내는 10~18까지의 범위에 있다고 하였으며, 이들도 지위지수 추정식으로 C-R 모델을 이용한 바 있다.

Fig. 2.

Site index diagram in Chamaecyparis obtusa forest.

3.3. 편백림의 임분수확표 작성

국가산림조사 자료에 기반한 편백림의 임분수확표는 다음과 같이 도출되었다(예, 지위지수 14). 이 수확표는 정상적인 임분생장 및 임분구조를 갖는 법정림 개념의 임분수확표가 아니고 현실 산림을 반영한 임분생장과 구조를 갖는 경험적 임분수확표라 볼 수 있다.

Table 5에서 편백림의 연평균생장량은 30년일 때 최고의 생장량을 보여, Yoon et al.(2021)이 국내 침엽수류 중 중부지방소나무는 34년, 일본잎갈나무 35년, 리기다소나무 31년으로, 침엽수는 평균 33년에 이를 때 최대시기에 도달하는 것이라 보고한 바 있는데, 이와 유사한 결과였다.

Table 5.

Empirical stand yield table in Chamaecyparis obtusa forest (SI, 14)

또한 Jung et al.(2020)에 의하면, 편백림에 대한 기존 수확표(Lee et al., 2009) 상 생장량과의 비교(지위 14 기준)에서, 기존 결과보다 재적량이 높게 나타났다고 하였으며, 이번 우리가 분석한 결과는 Jung et al.(2020) 연구보다 더 높게 산정되었다. 이 같은 결과는 기존 임분수확표의 재적산정 시 국립산림과학원이 새롭게 만든 수간곡선식에 의한 정보를 반영하지 않았기 때문이다. 즉, 최근의 수간곡선식에 의한 수종별 재적산정에 따르면 기존 1970-80년대 재적산정 결과보다, 현실림 반영에 따라 대부분의 수종에서 높은 재적값이 산출되었기 때문이다.

4. 결 론

본 연구는 우리나라 남부권역의 주요 수종인 편백림에 대한 임분수확표를 Weibull직경분포모델을 이용하여 작성하였다. 분석에는 국가산림자원조사 표본점 자료를 활용함으로써 현실림을 반영한 경험적 임분수확표를 만들고자 하였다. 그리고 임분수확표는 산림경영 대상지에서 활용될 것이므로 조사 표본점 중 시업지의 산림생장자료 및 각종 이상치를 기각하여 분석, 연구 수행함으로써 산주와 산림정책 담당자에게 산림경영의사결정에 도움이 되고자 하였다. 현실림 자료를 활용한 사전 연구도 수행된 바 있으나, 앞서 언급한 NFI 상 시업지 및 경영가능한 표준지만의 자료를 활용한 본 연구과는 차이가 있는 것이다.

직경분포모델을 적용시켜 임분수확을 예측하기 위해 도출된 임분 흉고단면적, 흉고직경, 수고, 최소 및 최대 직경 등의 생장식은 모두 적합도 지수가 5% 수준에서 유의성이 있었으며, 임분생장을 해석하기 위해 가장 중요한 인자 중의 하나인 지위지수 추정모델은 C-R 식을 적용시켰다. C-R 모델이 적합도 지수, 오차, 편의 등의 통계량 모두 Schumacher 모델보다 우수하여 이를 최적모델로 선택한 것이다.

지위지수와 임령을 기준으로 직경 및 수고, 재적생장량 등의 정보를 제공하고, 재적수확최대벌기령 산출 시 이용되는 연평균생장량 등의 정보까지를 제공하는 이번 임분수확표는 현재 우리나라 편백림의 생장량 뿐만아니라 미래의 생장량까지를 제시하고자 하였다. 또한 Weibull 직경분포모델 적용에 따라 각 임령별로 직경급별 입목본수의 분포 및 재적분포 까지의 정보를 제공하는 임분수확표로 만들었다. 이러한 결과들은 분석에 사용되는 자료의 범위, 시기, 적용 추정식 등에 따라 각기 다른 결과들을 제시할 수도 있을 것이다. 그러나 국가에서 공인한 NFI자료를 이용함은 현실림을 제대로 반영한 것이고, 이 자료에서 약간 부족인 유령림 및 노령림의 자료까지의 보완은 현재까지 이러한 분석 결과 중에서 최고의 정도를 보여 주었다고 생각된다.

향후 국가산림조사가 지속적 수행되고 조사자료의 DB가 누적되면, 다시 새로운 임분수확표의 개념 도입 또는 추정모델을 적용시켜, 보다 정밀도 높고 현실림을 맞춤 반영하는 분석이 이루어지기를 기대한다.

Acknowledgments

본 연구는 산림청 일반연구사업(과제번호: SC0600-2021-01)의 지원으로 수행된 일부 연구결과입니다.

REFERENCES

• Bailey, R. L., Dell, T. R., 1973, Quantifying diameter distributions with the weibull function, Forest Science, 19, 97-104.
• Buckman, R. E., 1962, Growth and yield of red pine in Minnesota, USDA, Forest Service, Technical Bulletin, No. 1272, 50.
• Cao, Q. V., Burkhart, H. E., 1984, A segmented distribution approach for modeling diameter frequency data, Forest Science, 30(1), 129-137.
• Chapman, D. G., 1961, Statistical problems in population dynamics. In Proc., Fourth Berkly Symposium on Mathematical Statistics and Probability, Univ Calif. Press, Berkly.
• Clutter, J. L., Fortson, J. C., Pienaar, L. V., Brister, G. H., Bailey, R. L., 1983, Timber management –A quantitative approach-, John Wiley & Sons, 333.
• Ek, A. R., Issos, J. N., Bailey, R. L., 1975, Solving for weibull diameter distribution parameters to obtain specified mean diameters, Forest Science, 21(3), 290-292.
• Forest Research Institute, 1962-1985, Yield tables and site index tables, Forest Research Institute, 49.
• Fries, J., 1974, Growth models for tree and stand simulation, Research notes 30, Royal College of Forestry, Stockholm, 397.
• Garcia, O., 1981, Simplified method-of-moments estimation for the Weibull distribution, New Zealand Journal of Forest Science, 11(3), 304-306.
• Hayashi, T., 1937, Stem volume table and breast-height form factor table in Kangwondo. etc., Forest Experiment Research Report, 10, 24-31.
• Jung, S. Y., Lee, K. S., Lee, H. S., Bae, E. J., Park, J. H., Ko, C. U., 2020, Development of stand yield table based on current growth characteristics of Chamaecyparis obtusa stands, Journal of Korean Society of Forest Science, 109(4), 477-483.
• Kang, J. T, Ko, C. U., 2020, The development of a stem taper equation and a stem table for standing trees of Chamaecyparis obtusa on Jeju island and in the southern regions of South Korea, The Journal of Korean Island, 32(4), 221-233. [https://doi.org/10.26840/JKI.32.4.221]
• Kang, S. P., Kim, J. Y., An, K. W., 2015, Site index estimation and suitable-land evaluation of Cryptomeria japonica and Chamaecyparis Obtusa -focused on Jeju special self-governing province and southern regions-, The Journal of Korean Island, 27(3), 125-144.
• Kim, C. R., 2000, SAS, a statistic box, Data Plus, 592.
• Kim, D. C., Yoo, J. W., 1977, A Study on the growth and yield of Cryptomeria, Japanese Cypress stand, Research reports of Forest Research Institute, 24, 5-30.
• Leary, R. A., 1991, Near-normal, empirical, and identity yield tables for estimating stand growth, Canadian Journal of Forest Research, 21, 353-362. [https://doi.org/10.1139/x91-043]
• Lee, K. H., Chung, Y. G., Son, Y. M., 1996, Forest growth and yield prediction model, Forestry Research Institute, Research report No. 127, 142.
• Lee, K. H., Son, Y. M., Bae, S. W., 2009, Tree volume, weight and stand yield table, National Institute of Forest Science, 271.
• Lee, H. G., Yoo, J. W., Noh, G. H., Kim, S. I., 1985, A Study on the yield and growth of Pinus thunberggi stand, Forestry Research Institute, Research report, 32, 49-60.
• Liu, C., Zhang, L., Davis, C. J., Solomon, D. S., Gove, J. H., 2002, A Finite mixture model for characterizing the diameter distributions of mixed-species forest stands, Forest Science, 48(4), 653-661. [https://doi.org/10.1093/forestscience/48.4.653]
• Monserud, R. A., 1984, Height growth and site index curves for inland douglas-fir based on stem analysis data and forest habitat type, Forest Science, 30(4), 943-965.
• National Institute of Forest Science (NIFoS), 2009, Volume · weight table and stand yield table, NIFoS, 265.
• National Institute of Forest Science (NIFoS), 2012, Tree volume · biomass and stand yield table, NIFoS, 261.
• National Institute of Forest Science (NIFoS), 2023, 2023 standing tree volume · biomass and stand yield table, NIFoS, 377.
• Park, J. H., Son, Y. M., Lee, K. S., Park, E. J., Jung, S. Y., 2019, The adequacy assessment and growth effects by methods of 1st thinning in Chamaecyparis obtusa forest, Journal of Korean Society of Forest Science, 108(3), 349-356.
• Park, J. H., Yoo, B. O., Lee, K. S., Park, Y. B., Kim, H. H., Jung, S. Y., 2018, Prediction of mortality and yield for Chamaecyparis obtusa using stand density management diagram, Journal of Korean Society of Forest Science, 107(2), 174-183.
• Peng, C. H., 2000, Growth and yield models for uneven-aged stands: Past, present and future, Forest Ecology and Management, 132(2-3), 259-279. [https://doi.org/10.1016/S0378-1127(99)00229-7]
• Richards, F. J., 1959, A Fexible growth function for empirical use, Journal of Experimental Botany, 10, 290-300. [https://doi.org/10.1093/jxb/10.2.290]
• Schumacher, F. X., 1939, A New growth curve and its application in timber yield studies, Journal of Forestry, 37, 819-820.
• Son, Y. M., Lee, K. H., Kwon, S. D., Lee, W. K., 2004, Forest value assessment and prediction by major species. Research reports of Korea Forest Research Institute, 04-01, 125.
• Son, Y. M., Pyo, J. K., Kim, S. W., Lee, K. H., 2012, Prediction of stand volume and carbon stock for Quercus variabilis using Weibull distribution model, Journal of Korean Society of Forest Science, 101(4), 599-605.
• Spurr, S. H., 1952, Forest inventory, The Ronald Press Co.: Digitized, Nov. 9, 2011, New York, 476.
• Vanclay, K., 1994, Modeling forest growth and yield; Applications to mixed tropical forests, 312.
• Vuokila, Y., 1965, Functions for variable density yield tables of pine based on temporary sample plots, Metsatieteellisen tutkimuslaitoksen julkaisuja, 60(4), 86-234.
• Yoon, H., Bae, E. J., Son, Y. M., 2021, Growth curve estimation of stand volume by major species and forest type on actual forest in Korea, Journal of Korean Society of Forest Science, 110(4), 648-657.